
Power Factor Correction
(Concept of Reactive Power)
Reactive power refers to the electrical power used by electrical equipment to establish and maintain electric and magnetic fields. It is employed for the exchange of electric and magnetic fields within a circuit. Instead of performing work externally, it exchanges energy back and forth between the power source and inductive or capacitive loads, thus being a type of power with no energy consumption. The formula for reactive power isQ=U×I×sinφ, where U represents the effective value of voltage, I denotes the effective value of current, and sinφ is the sine of the phase difference between voltage and current.
(Power Factor)
Apparent power (S) is the product of the voltage vector (U) and the current vector (I). In a sinusoidal AC circuit, apparent power, active power (P), and reactive power (Q) satisfy the Pythagorean theorem, which is expressed as S² = P² + Q². Additionally, the power factor cosφ = P/S (where φ is the phase difference between voltage and current).
(Generation of Reactive Power)
Many electrical devices (such as asynchronous motors, transformers, etc.) are mostly inductive loads. During operation, inductive loads require reactive power to establish and maintain magnetic fields. Their current lags behind the voltage, and they draw a large amount of reactive power during operation. This leads to a decrease in the power factor of the system, an increase in ineffective current, higher electricity costs for users, and a heavier load on the power consumption system. When there are significant harmonics in the power consumption system, distorted reactive power will also show obvious characteristics.
(Reactive Power Compensation)
According to the mathematical expression Q = UI × sinφ, for inductive loads, the current lags behind the voltage, so the value of sinφ is greater than zero, and they absorb reactive power. For capacitive loads, the current leads the voltage, so the value of sinφ is less than zero, and they generate reactive power. When capacitive loads (such as capacitors) are connected in parallel to a circuit containing inductive loads, the capacitive reactive power provided by the capacitors can compensate for part of the inductive reactive power absorbed by the inductive loads. This reduces the total amount of reactive power that needs to be supplied by the original line, thereby achieving the effect of reactive power compensation.
(Example)
In a 400V three-phase system:
When cosφ = 1: The transmission of 500kW active power requires a current of 722A.
When cosφ = 0.6: The transmission of 500kW active power requires a current of 1203A.
Therefore, for power distribution and transmission equipment such as power supply transformers, capacitor configuration should be adopted to improve the power factor.
(Calculation of Compensation Capacity)
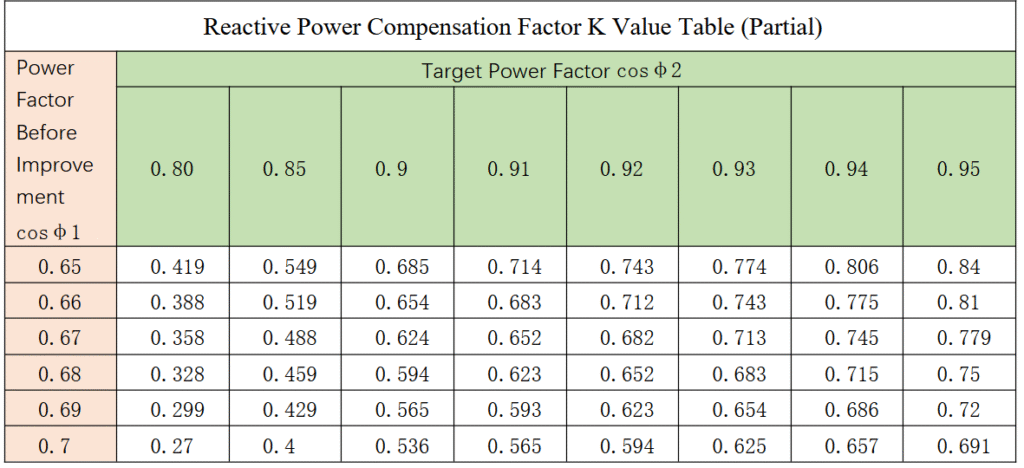
Example: The actual active power consumption is P = 550 kW, the natural power factor is 0.70, and the target power factor is 0.93. The compensation factor K from the table is 0.62, so the required compensation capacity is: 550 × 0.62 = 341 (kvar).
Note: The installed capacity of the complete set of equipment should consider a capacity margin of about 1.2~1.A based on the fundamental wave compensation capacity.
Before compensation: 550 / 0.70 = 785.7 (kVA), so an 800 kVA transformer needs to be selected.
After compensation: 550 / 0.93 = 591.4 (kVA), so a 630 kVA transformer needs to be selected.
Reduction in losses before and after compensation: 1 – (0.70 / 0.93)^2 = 43.3%
